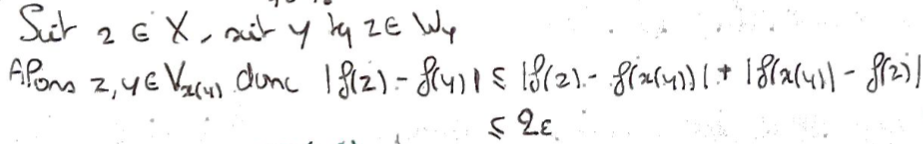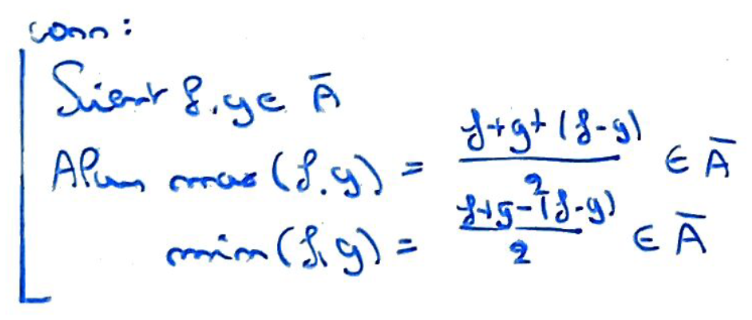\(\overline A\) est complet en tant que Fermé d'un complet.

\(\overline A\) est une Algèbre par continuité des opérations, donc il reste juste à montrer qu'elle est unitaire.

Pour tout point \(x\), on prend \(f_x\) qui ne s'y annule pas, et \(V_x\) l'ensemble des points où \(f_x\) ne s'annule pas.

Ce sont des ouverts qui recouvrent \(X\) \(\to\) par Compacité, on peut en extraire un sous-recouvrement fini.

Si on pose la somme des \(f_{x_i}^2\) (somme finie), alors cette somme continue et strictement positive sur \(X\), et donc est \(\geqslant\varepsilon\) pour un certain \(\varepsilon\).

Quitte à multiplier par un scalaire, on peut supposer \(f\leqslant1\).

On peut alors obtenir l'unité en multipliant \(f\times\frac1f\), et en approchant \(\frac1f\) par la Série entière (rayon de convergence ok via l'étape précédente).

Cette série est bien dans \(\overline A\) en tant que limite d'éléments de \(A\) (sommes partielles).

On peut supposer \(f\leqslant1\).

Pour \(\varepsilon\gt 0\) quelconque, on peut alors approcher \(\sqrt{f+\varepsilon}\) via la Série entière.

On peut alors obtenir \(\sqrt f\) comme une limite uniforme lorsque \(\varepsilon\to0\).

Si \(f\) est positive, on peut la supposer \(\leqslant1\).

On peut alors approcher \(\frac1f\) via la Série entière.

Si \(f\) est négative, on peut écrire \(\frac1f=\frac f{f^2}\), et conclure par positivité de \(f^2\).

En suivant les hypothèses du théorème de Stone-Weierstrass, on peut prendre pour tout \(y\in X\setminus V\) une fonction qui n'est pas égale en \(x\) et en \(y\).

On peut supposer que cette fonction vaut \(0\) en \(y\) et \(1\) en \(x\).

On peut alors poser pour tout \(y\) l'ensemble des points qui ont une image par \(g_y\) \(\lt \varepsilon\) \(\to\) ces ensembles sont Ouverts et contiennent \(y\).

Ils forment donc un Recouvrement ouvert, dont on peut extraire un sous-recouvrement par Compacité.

On pose \(g\), formée du \(g_{y_i}\) minimal qu'on borne entre \(\frac\varepsilon2\) et \(1-\frac\varepsilon2\).

En prenant \(\varepsilon\) assez petit, on a alors \(g(z)\leqslant\varepsilon\) pour tout \(z\notin v\).

En prenant \(f\in A\) assez proche de \(g\) (ok par Adhérence de \(\overline A\) pour \(A\)), on trouve \(f\) qui respecte les conditions voulues.

Cela revient à montrer que pour toute fonction continue, il existe une fonction de \(A\) arbitrairement proche.

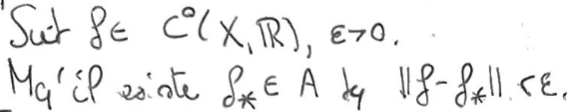
Quitte à faire un changement de variable affine (ok parce qu'on a montré que \(1\in A\)), on peut considérer \(0\leqslant f\leqslant 1\).

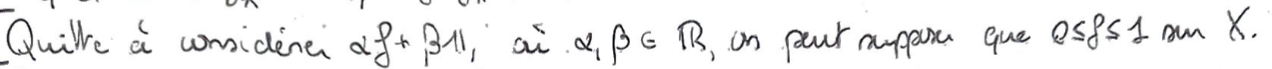
Par continuité de \(f\), pour tout \(x\in X\), on pose \(V_x\) l'ensemble des \(y\) tels que \(\lvert f(x)-f(y)\rvert\lt \varepsilon\) \(\to\) c'est un voisinage ouvert de \(x\).

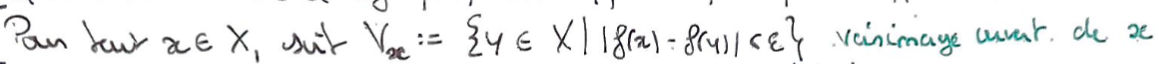
Ces voisinages forment un recouvrement, dont on peut extraire un sous-recouvrement fini par compacité de \(X\).

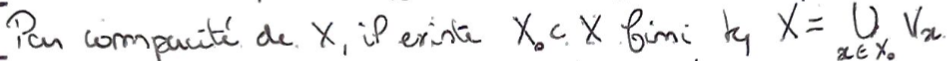
Pour \(y\in X\) on pose \(x(y)\) l'indice \(x\) donnant le voisinage \(V_x\) correspondant à \(y\).

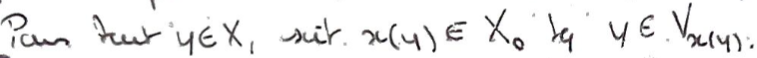
En utilisant le lemme précédent, on pose \(0\leqslant\varphi_y\leqslant1\) tq \(\varphi_y(y)\geqslant1-\varepsilon\) et \(\varphi_y\leqslant\varepsilon\) en dehors de \(V_{x(y)}\).

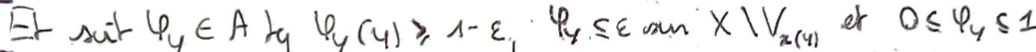
On pose \(W_y\) l'ensemble des \(z\) tq \(\varphi_y(z)\geqslant\varepsilon\).

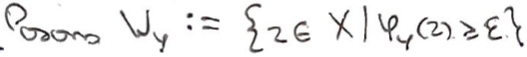
C'est un recouvrement ouvert de \(X\), dont on peut extraire un sous-recouvrement fini par compacité.

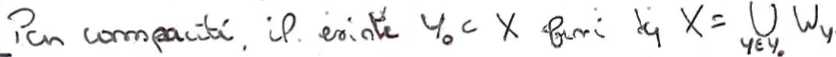
On pose \(f_*:z\mapsto\max_{y\in Y_0}f(y)\varphi_y(z)\).

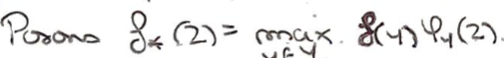
Pour \(z\in X\) tq \(z\in W_y\), on montre que \(\lvert f(z)-f(y)\rvert\) est arbitrairement petit en utilisant le fait qu'ils sont \(\in V_{x(y)}\).
1

Cela nous permet de minorer \(f_*(z)\) et de montrer qu'il est arbitrairement proche de \(f(z)\).
1

On peut également faire une majoration et montrer qu'ils sont aussi arbitrairement proches dans ce sens.
1

On a donc trouvé \(f_*\in \overline A\) arbitrairement proche de \(f\), ce qui nous permet de conclure.


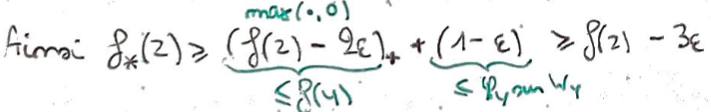
1

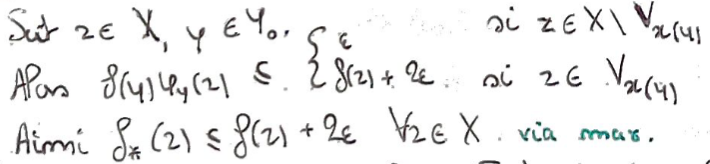
1

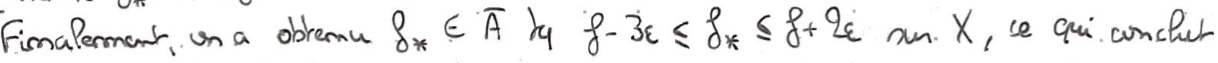
1

On veut utiliser le Théorème de Stone-Weierstrass.

L'ensemble étudié est une Algèbre, car c'est un Espace vectoriel stable par le produit.

On montre que cette algèbre

Les fonctions constantes ne s'annulent pas, ce qui permet de valider la deuxième hypothèse et de conclure.

\(K\) est séparable car métrique compact, donc précompact.

On considère la Sous-algèbre formée de les applications qui donnent la distance entre l'argument et un point de la suite, auquel on ajoute la fonction \(1\) comme élément neutre.

\(\mathcal A\) est donc formée de polynômes de telles applications.

On vérifie que cette algèbre sépare les points de \(K\) en utilisant la densité des \(a_n\) et l'\(\ne\!\!\!\triangle\).

Par Compacité de \(K\), le Théorème de Stone-Weierstrass nous donne la Densité de \(\mathcal A\) dans \(\mathcal C(K)\).

En se restreignant aux polynômes à coefficient dans \({\Bbb Q}\), on a toujours la Densité, mais aussi la dénombrabilité, ce qui nous donne la séparabilité

On pose \(B\) l'ensemble des parties réelles des fonctions de \(A\), en prenant \(\frac{f+\bar f}2\).

\(B\) satisfait Théorème de Stone-Weierstrass réel, donc \(\overline B=\mathcal C^0(X,{\Bbb R})\).

On peut faire de même avec la partie imaginaire, ce qui nous permet de conclure.